Learning Pose Estimation for UAV Autonomous Navigation and Landing Using Visual-Inertial Sensor Data
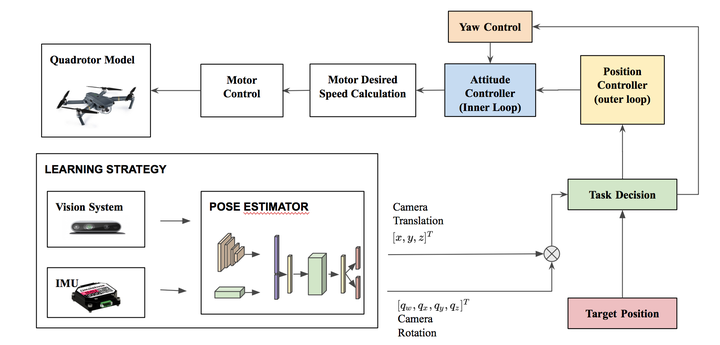 Learning Estimator
Learning EstimatorLocalization is an essential task for robotics applications. To know the exact pose (position and orientation) of the agent it’s essential for visualization, navigation, prediction, and planning.
We propose a new end-to-end approach for online pose estimation that leverages multimodal fusion learning. This consists of a convolutional neural network for image regression and two long short-term memories (LSTMs) of different sizes to account for both sequential and temporal relationships of the input data streams. A small LSTM architecture integrates arrays of acceleration and angular velocity from the inertial measurements unit sensor. A bigger core LSTM processes visual and inertial feature representations along with the previous vehicle’s pose and returns position and orientation estimates at any given time.
Estimation Problem
Given the actual pose state
The inputs for our model are observation tuples
The online localization task aims to estimate the pose of the vehicle
In the learning framework, we aim to model the mapping
$ xt = f(x{t-1}, y_{t-1}) $,
where
The architecture

Image feature extractor
To encode image features, we use ResNet18, pre-trained on the ImageNet dataset, truncated before the last average pooling layer. Each of the convolutions is followed by batch normalization and the Rectified Linear Unit (ReLU).
We replace the average pooling with global average pooling and subsequently add two inner-product layers. The output is a visual feature vector representation
Inertial feature extraction
IMU measurements are generally available at a rate of an order of magnitude higher (e.g.,
Intermediate fully-connected layer
The inertial feature vector
This vector is then carried over to the core LSTM for sequential modeling.
Core LSTM
The core LSTM takes as input the motion feature
$zt
and models the dynamics and the connections between sequences of features, where $ h_t = f(zt, h{t-1})$
The use of the LSTM module allows for the rapid deployment of visual-inertial pose tracking. These models can maintain the memory of the hidden states over time and have feedback loops among them. In this way, they enable their hidden state to be related to the previous one, allowing them to learn the connection between the last input and pose state in the sequence.
The output of the LSTM is carried into a fully-connected layer, which serves as an odometry estimation. The first inner-product layer is of dimension
$ x_t = LSTM( zt , h{t-1} ) $.
The Criterion
We predict the position and orientation of the robot following the work of Kendall et al., with the following modification[kendall2017geometric]. In our loss function, we introduce an additional constraint that penalizes both the
Our loss function is as follows:
where
The final loss function is as follows:
where